O Oscilador Harmônico Relativístico

Alguns problemas na física, embora pareçam  triviais são de grande utilidade e podem ser aplicados em diversas situações. Um exemplo de um problema que, a primeira vista, é trivial e sem utilidade é o do Oscilador Harmônico Simples. Basicamente constitui-se de um sistema massa-mola. Um corpo preso a uma mola que se encontra fixa em uma parede rígida. É claro que existe uma posição de equilíbrio onde o sistema tem a menor energia possível. Essa posição é aquela em que o corpo se encontra em repouso e por isso a resultante das forças que atuam sobre ele é nula. Porem, se alguém comprimir, ou esticar a mola uma força surgirá e atuará no sentido contrário daquele que a pessoa empurrou. Se depois que o corpo for empurrado o mesmo for solto, ele iniciará um movimento perpetuado, oscilando entorno do ponto de equilíbrio. Por exemplo: se comprimirmos uma mola, de modo que a diferença entre a posição de equilíbrio e a posição que vamos abandonar a mola seja 20 cm. A mola iniciará uma oscilação em torno do ponto de equilíbrio ou seja, abandonamos a 20 cm do ponto desse ponto o corpo volta na direção do ponto de equilíbrio, passa do mesmo, anda mais 20 cm para o lado contrário que o abandonamos e depois volta para o ponto de equilíbrio e continuará nesse movimento oscilatório em torno do ponto de equilíbrio.

O físico inglês R. Hooke descobriu uma expressão para calcular essa tal força que "puxa" o bloco em direção do ponto de equilíbrio. Hooke descobriu que:

F = -k.Δl (Lei de Hooke)

Onde F é a força que a mola exerce no corpo, k é uma constante chamada de constante da mola, e Δl é a diferença entre a posição em que o corpo se encontra e a posição de equilíbrio. Podemos simplificar e impor que a posição de equilibro seja no ponto zero. Desse modo a força é dada por:

F=-kx

Onde x é a posição em que o corpo se encontra. É importante informar que essa posição na qual me refiro desde o inicio do post é a posição medida usando um eixo paralelo a mola. 

Como a força elástica é a única que age no corpo na direção do eixo que estamos trabalhando, e na direção perpendicular a esse eixo a força peso e a reação normal de apoio se cancelam, podemos dizer que a força elástica é igual a força resultante. Porem sabemos que a força resultante clássica vale a taxa de variação do momento linear com relação ao tempo. Formalizando matematicamente e usando a função módulo:

F=dp/dt , p=mv  --> F= m dv/dt ; v=dx/dt ; --> F= m d²/dt² (x) 

Resumindo: Aplicamos o operador d²/dt² na posição e multiplicamos pela massa. Então teremos o módulo da força resultante. 

Como a força F é igual a força elástica, então seu módulo também é. desse modo podemos escrever:

F+Kx=0 = m d²/dt² (x) + kx 

Podemos definir um operador L como sendo:

L=m d²/dt² + k  

Dessa maneira :

Lx=0 

Tudo que precisamos fazer é achar a função que quando o operador L é aplicado tenham seus auto valor nulo. 

Quando acharmos tal função , teremos a posição em função do tempo, do corpo, em qualquer instante de tempo t. 

Se traçarmos o gráfico da posição em função do tempo, teremos algo semelhante a:

Porem, na Relatividade Especial a força não é dada do mesmo modo que na mecânica clássica. Desse modo o operador L não é o mesmo. Pode-se demonstrar que o novo operador L' , Válido na relatividade Especial é dado por:

L'=d(v)m d²/dt² + k  , onde d(v) é uma função bem definida.

Desse modo, a equação de auto valor correta é:

L' x =0 

Devemos procurar a função, ou as funções que quando o operador L' seja aplicado na mesma, tenha seus autovalores nulos. 

Se formos procurar tais funções, veremos que elas são muito parecidas com a do caso clássico quando estamos em um mundo de baixas velocidades, comparando com a velocidade da luz, porem são bastante diferentes quando estamos em um mundo de altas velocidades. 

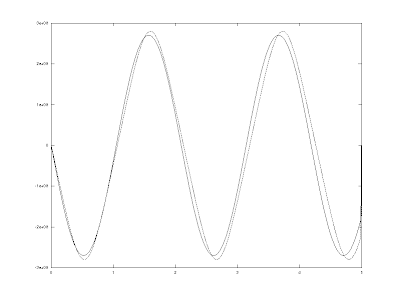
Vamos postar agora alguns gráficos, respectivamente, da posição,velocidade,aceleração, todas em função do tempo com fracões diferentes da velocidade da luz

A linha tracejada é obtida a partir do caso relativístico, enquanto a linha continua é obtida a partir do caso clássico.

Primeiro as posições em função do tempo:

Esse primeiro gráfico é com v=o,3c , onde c é a velocidade da luz e v é a velocidade inicial do oscilador. 

Note que o caso relativístico e clássico, embora apresentem soluções diferentes para a equação dos autovalores, são apenas ligeiramente diferente.

Essa segunda é com v=0,95c. Note que a funções do caso clássico e relativístico são muito distintas e que a função relativística tem sempre amplitude maior.

Para v=0,9999c já não conseguimos mais ver o segundo "pico" da função. Vale lembrar que o valor da função nesses picos vale a amplitude da função. 

Agora as respectivas velocidades em função do tempo para as mesmas frações da velocidade da luz:

A senoide é cada vez mais "esticada" e as funções são cada vez mais distintas.

A aceleração em função do tempo, também para as mesmas fraçoes de c:

Note que cada vez que aumentamos a fração as funções ficam muito distintas, a aceleração vai tendendo para funções do tipo Delta de Dirac , cada vez mais espaçadas, de modo que com 0,9999c não chegamos a ver nem o primeiro pico.